Reaktionsgeschwindigkeit und -ordnung
IMPP-Score: 0.8
Grundlagen der Reaktionsgeschwindigkeit und Reaktionskinetik
Bevor wir uns mit den spezifischen Reaktionsordnungen beschäftigen, müssen wir ein fundiertes Verständnis der Reaktionsgeschwindigkeit aufbauen. Die Reaktionsgeschwindigkeit gibt an, wie schnell eine chemische Reaktion abläuft. Sie ist definiert als die Änderungsrate der Konzentration eines Reaktanden (meist der Edukte) oder eines Produkts pro Zeiteinheit. Die Reaktionsgeschwindigkeit ist also ein Maß dafür, wie viel Substanz in einer bestimmten Zeit umgesetzt wird.
Gehe immer davon aus, dass die Reaktionsgeschwindigkeit vom Verbrauch der Reaktanden und damit von der Abnahme ihrer Konzentration abhängt.
Der geschwindigkeitsbestimmende Schritt
In einer Reaktionssequenz gibt es manchmal Schritte, die schneller, und solche, die langsamer ablaufen. Der langsamste dieser Schritte ist der geschwindigkeitsbestimmende Schritt. Er legt fest, wie schnell die gesamte Reaktion fortschreiten kann, ähnlich wie der langsamste Läufer in einer Staffel den Erfolg des gesamten Teams bestimmt.
Das IMPP fragt besonders gerne nach dem geschwindigkeitsbestimmenden Schritt und dessen Einfluss auf die Gesamtreaktion. Es ist also wichtig, diesen Begriff zu verstehen und zu erkennen.
Reaktionsordnungen und ihre Geschwindigkeitsgesetze
Die Reaktionsordnung beschreibt, wie die Reaktionsgeschwindigkeit von der Konzentration der Reaktanden abhängt. Es gibt Reaktionen 0., 1. und 2. Ordnung, die eine besonders wichtige Rolle spielen.
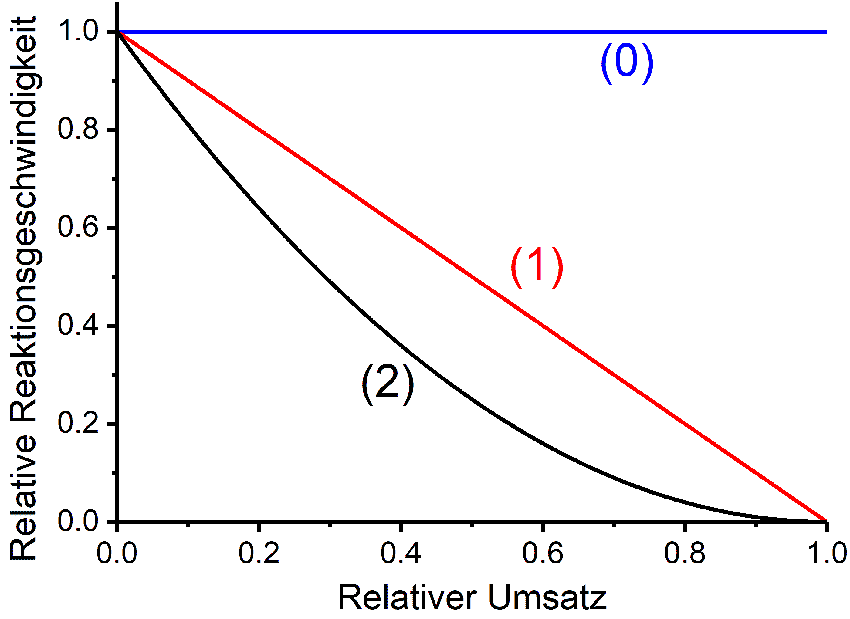
Reaktionen 0. Ordnung
Bei einer Reaktion nullter Ordnung ist die Reaktionsgeschwindigkeit konstant und unabhängig von den Konzentrationen der reagierenden Stoffe. Die Konzentration der Edukte nimmt linear mit der Zeit ab. Dies bedeutet, dass die Menge der umgesetzten Substanz pro Zeitintervall gleich bleibt.
Geschwindigkeitsgesetz für Reaktionen 0. Ordnung: \[ v = k \] mit \(v\) als Reaktionsgeschwindigkeit und \(k\) als Geschwindigkeitskonstante.
Reaktionen 1. Ordnung
Reaktionen erster Ordnung zeigen eine Reaktionsgeschwindigkeit, die direkt proportional zur Konzentration des reagierenden Stoffes ist. Hier nehmen die Konzentrationen exponentiell ab, und die Halbwertszeit ist konstant und unabhängig von der Anfangskonzentration.
Geschwindigkeitsgesetz für Reaktionen 1. Ordnung: \[ v = k \cdot [\text{A}] \] mit \([\text{A}]\) als die Konzentration des Edukts.
Beachte, dass bei Reaktionen erster Ordnung die Halbwertszeit konstant ist: \[ t_{1/2} = \frac{\ln(2)}{k} \] Das ist ein beliebtes Prüfungsthema!
Reaktionen 2. Ordnung
Bei Reaktionen zweiter Ordnung hängt die Reaktionsgeschwindigkeit entweder vom Quadrat der Konzentration eines Reaktanden oder vom Produkt der Konzentrationen zweier verschiedener Reaktanden ab. Die Halbwertszeit ist hier nicht konstant, sondern abhängig von der Anfangskonzentration der Reaktanden.
Geschwindigkeitsgesetz für Reaktionen 2. Ordnung: \[ v = k \cdot [\text{A}] \cdot [\text{B}] \] für eine bimolekulare Reaktion, oder \[ v = k \cdot [\text{A}]^2 \] für eine unimolekulare Reaktion mit zweiter Ordnung.
Beispiele Reaktionsordnungen
Beispiel Reaktion 0. Ordnung:
- Konstante Abnahme: Bei einer festen Rate wird unabhängig von der Konzentration eine gleichbleibende Menge an Substanz pro Zeiteinheit umgesetzt.
Beispiel Reaktion 1. Ordnung:
- Exponentieller Verfall: Die Konzentration eines Stoffes verringert sich exponentiell mit konstanten Halbwertszeiten.
Beispiel Reaktion 2. Ordnung:
- Konzentrationsabhängige Halbwertszeit: Die Halbwertszeit hängt von der Anfangskonzentration der Reaktanden ab und ist nicht konstant.
Temperaturabhängigkeit und Arrhenius-Gleichung
Die Arrhenius-Gleichung verbindet die Geschwindigkeitskonstante \(k\) mit der Temperatur \(T\). Sie zeigt, dass die Reaktionsgeschwindigkeit mit steigender Temperatur zunimmt. Katalysatoren wiederum erhöhen die Geschwindigkeit einer chemischen Reaktion, ohne die Reaktionsordnung zu ändern.
\[ k = A \cdot e^{-\frac{E_a}{RT}} \] mit \(A\) als präexponentiellem Faktor, \(E_a\) als Aktivierungsenergie, \(R\) als universeller Gaskonstante und \(T\) als Temperatur in Kelvin.
Das Verständnis der Arrhenius-Gleichung ist entscheidend, da sie dir zeigt, wie die Reaktionsgeschwindigkeit mit der Temperatur skaliert. Ein klassischer Punkt, den das IMPP in Prüfungen aufgreifen könnte.
Zusammenfassung
Feedback
Melde uns Fehler und Verbesserungsvorschläge zur aktuellen Seite über dieses Formular. Vielen Dank ❤️
Footnotes
Credits Reaktionsordnungen Grafik: Espresso robusta, Relative Reaktionsgeschwindigkeiten, CC BY-SA 4.0↩︎
